Programmation PYTHON en Sciences

Des programmes en Python pouvant être utilisés en SPC.

Tracé de graphique, incertitude, régression linéaire, période, modélisation, équation de droite, tracé de vecteurs, de variation de vecteurs; réactifs limitants, fct sinusoïde ,angle de réfraction, grossissement : de nombreux domaines sont programmables.

Cf Partie PYTHON en SPC avec Jupyter Notebook

Python en SPC avec Collab de Google

Un compte Google ( en gmail ) permet d'activer Google Collaboratory permettant la conception mais aussi le fonctionnement en live des "cellules programmes" après avoir importé tous les fichiers ( ipynb, csv, image ...)
Les fichiers sont visibles dans la fenêtre de droite, les fichiers crées dans la fenêtre de gauche; ... super pratique !

cf Partie Python en SNT avec Jupyter Notebook

A la section SNT du Site Ella Science , le traitement de données et la géolocalisation se prête à l'emploi de Python sous Jupyter Notebook !

Partie expérimentale de Python avec Thonny

L'Interpréteur PYTHON choisi est THONNY

Attention à importer les librairies sous Thonny, parfois à chaque connexion élève !

Attention à l'indentation ( décalage sous If )...bonne chance !

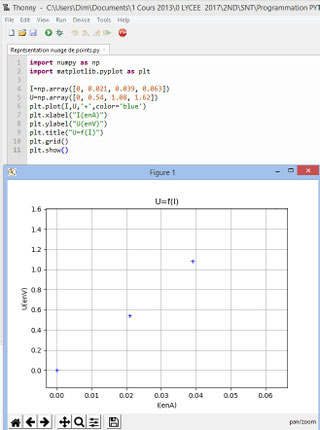
Tracé de graphique

Dans Tool>Manage packages : importer numpy et matplotlib

import numpy as np
import matplotlib.pyplot as plt

I=np.array([0, 0.021, 0.039, 0.063])
U=np.array([0, 0.54, 1.08, 1.62])
plt.plot(I,U,'+',color='blue')
plt.xlabel("I(enA)")
plt.ylabel("U(enV)")
plt.title("U=f(I)")
plt.grid()
plt.show()

A FAIRE : Représenter un NUAGE de POINTS de vos données expérimentales

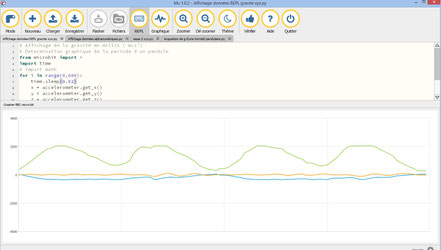
Pendule : Acquisition de Périodes d'une micro:bit pendulaire

A FAIRE :

Rechercher des paramètres influençant la période d'oscillation d'un pendule
Étude dimensionnelle
Programmation Python avec Plotter sous Mu editor
Acquisition du champ g selon les 3 axes x,y,z
Tracé et Exploitation
Modélisation
Vérification

Programme

for i in range(0,600):
    time.sleep(0.02)
    x = accelerometer.get_x()
    y = accelerometer.get_y()
    z = accelerometer.get_z()
    print((x, y, z))

Modélisation d'un graphique

import numpy as np
import matplotlib.pyplot as plt
import scipy as sc
from scipy.stats import linregress

I=np.array([0, 0.021, 0.039, 0.063])
U=np.array([0, 0.54, 1.08, 1.62])
plt.plot(I,U,'+',color='blue')
plt.xlabel("I( en A)")
plt.ylabel("U( en V)")
plt.title("U=f(I)")
plt.grid()
plt.show()
droite=sc.linregress(I,U)
coefficient=droite.slope
print("coefficient directeur :",coefficient)
oorigine=droite.intercept
print("ordonnée à l'origine:",oorigine)
Umodele=coefficient*I+oorigine
plt.plot(I,Umodele,color='red')

Tracé de l'équation horaire de la chute d'une tasse

Tracé de Vecteurs

Dans Tool>Manage packages : importer quiver

import numpy as np
import matplotlib.pyplot as plt

x=np.array([0,0,0,0])
y=np.array([1.698,1.691,1.674,1.643])
plt.plot(x,y,'o',markersize= 3)

N=4
Dt=0.035
for k in range (0,N-1) :
    vy=(y[k+1]-y[k])
    echelle=0.4
    vy=vy*echelle
    plt.quiver(x[k],y[k],0,vy,color='red', scale=1,scale_units='xy')
plt.xlabel("x (en m)")
plt.ylabel("y (en m)")
plt.title("Vecteurs vitesse")
plt.text(-0.046,1.65,"Echelle 1cm <-> 0.4 m/s", color="blue")
plt.grid()
plt.show()

A FAIRE

Changer les valeurs des coordonnées

Adapter l'échelle à vos valeurs

Réactif limitant

print("Soit l'Equation de la réaction : aA+bB -> Produits\n Entrer les valeurs des coefficients stoechiométriques a et b ")
a=float(input("a="))
b=float(input("b="))
print("Entrer les quantités intiales des réactifs A et B en mol")
nA=float( input("n0(A)="))
nB=float( input("n0(B)="))
if nA/a < nB/b:
print("A est le Réactif LIMITANT")
elif nA/a > nB/b:
print("B est le Réactif LIMITANT")

A FAIRE

Soit l'équation de la réaction : 4Fe+3O2 --> 2 Fe2O3

On mélange 8 mol de Fe et 9 mol de O2

Quel est le réactif limitant ?
Vérifier votre calcul avec le programme
Apporter des modifications afin de vérifier si le mélange est stœchiométrique.

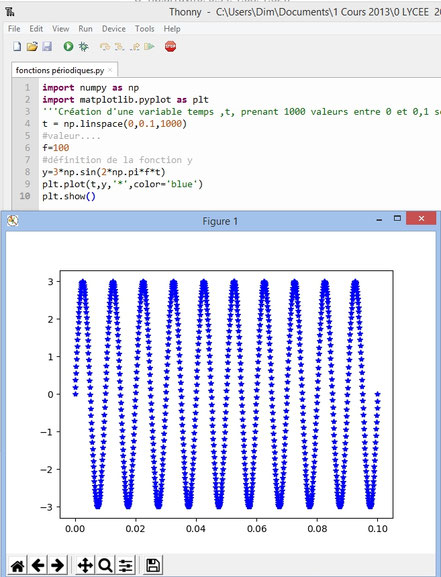
Fonction PERIODIQUE

Dans Tool>Manage packages : numpy

import numpy as np
import matplotlib.pyplot as plt
'''Création d'une variable temps ,t, prenant 1000 valeurs entre 0 et 0,1 secondes'''
t = np.linspace(0,0.1,1000)
#valeur....
f=100
#définition de la fonction y
y=3*np.sin(2*np.pi*f*t)
plt.plot(t,y,'*',color='blue')
plt.show()

A FAIRE

Ajouter des commentaires qui vous semble nécessaire
Ajouter à la fonction précédente la fonction y2=3*np.sin(4*np.pi*f*t)
Ajouter une fonction de période T = 0,020 s et d'amplitude égale à 4

Angle de réfraction

import numpy as np print('Ce programme va calculer un angle de réfraction\n
        
            connaissant _indice des milieux et l_angle d_incidence')
        
        i1=float( input("Quel est l'angle d'incidence?\n"))n1=float( input("Quel est l'indice de réfraction du
        
            milieu 1 ?\n"))
        
        n2=float( input("Quel est l'indice de réfraction du milieu 2 ?\n"))sini2=n1*np.sin(np.pi*i1/180)/n2 i2=np.arcsin(sini2) i2=180*i2/np.pi print("L'angle de réfraction vaut
        
            i2=",round(i2,2),"°.\n Le rayon réfléchi a pour angle ir=",i1,"°")

Grandissement

# Définition de la fonction qui ..............
def Fonction(AB,OA,OAp) :
    ApBp=AB*OAp/OA
    return ApBp
#Les valeurs sont données par l'utilisateur
AB=float(input("Donnez la taille de l'image AB en mètre : \n"))
OA=float(input("Donnez la distance OA en mètre : \n"))
AOprime =float(input("Donnez la distance OA' en mètre: \n"))
#Appel de la fonction qui .......
Fonction(AB,OA,OAp)
print("La taille de l'image est ",\
      Fonction(AB,OA,OAp,"m."))

Quinte en musique

A FAIRE :

Écrire une fonction permettant de calculer les fréquences successives des 12 premières quintes

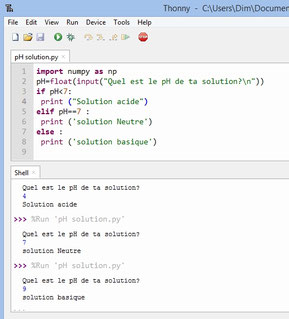
pH d'une solution

pH=float(input("Quel est le pH de ta solution?\n"))
if pH<7:
print ("Solution acide")
else :
print ('solution basique')

A FAIRE :

Écrire un programme donnant la nature d'une solution ( acide, neutre ou basique ) à partir du pH demandé
Modifier le programme dans le cas d'un pH égal à 7
Modifier le pour tester la valeur rentrée du pH [0-7]